티스토리 뷰
목차

학생들의 IQ와 대학입시 합격률 간의 관계를 알아보기 위해 3년간 총 1000명의 학생을 대상으로 하여 연구조사를 수행한 결과 다음과 같은 자료를 수집하였다.

1) 학생들의 IQ를 고려하지 않고 또한 별다른 추가적인 정보가 주어지지 않았다고 가정한다. 임의 의 한 학생을 선정했을 때 그 학생이 대학에 합격할 확률은 얼마인가?
* 단순 확률: 하나의 특정 사건이 일어날 확률.
표본공간을 S라고 했을 때 S의 부분집합 사건 A가 다음 성질을 만족하면 P(A)를 사건 A의 확률이라고 부름

합격할 확률: 52%
2) 200명의 학생 중 임의로 한 학생을 택했을 때, 그 학생의 IQ가 125를 넘을 확률은 얼마인가?

IQ가 125를 넘을 확률: 44%
3) 임의의 한 학생을 선정했을 때 그 학생이 대학에 합격했을 뿐만 아니라 IQ도 125를 넘을 확률은 얼마인가?
* 결합 확률: 둘 이상의 특정 사건이 동시에 일어날 확률.
A=대학합격, B=IQ125이상

약 22.9% 확률
4) 임의의 한 학생을 선정했을 때 그 학생이 대학에 합격했지만 IQ는 125를 넘지 않을 확률은 얼마인가?
A=대학합격, B=IQ125미만

약 29.1% 확률
5) 무작위로 한 학생을 뽑았더니, 그 학생의 IQ가 125 미만이라는 것이 알려졌다. 이 학생이 대학에 입학할 확률은 얼마인가?
조건부 확률 : 어떤 사건이 이미 발생했다는 전제하에 또 다른 사건이 발생할 확률
사전에 어떤 사건 A에 대한 사전확률이 부여된 상태에서 어떤 사건 B에 관한 정보가 알려진 후 그 사건 A에 관한 수정확률을 구할 때 사용.
A=대학합격, B=IQ125미만

약 42.6% 확률
6) 임의로 택한 한 학생이 대학에 합격했다고 자신을 소개했다. 이 학생의 IQ가 125 미만일 확률은 얼마인가?
A=대학합격, B=IQ125미만

약 46.2% 확률
7) 임의로 택한 한 학생의 IQ가 125 이상이라는 정보가 제공되었다. 학생들의 IQ를 고려하지 않고 또한 별다른 추가적인 정보가 주어지지 않았다면, 임의로 택한 한 학생이 대학에 합격할 확률은 0.55 또는 55%이다. 그렇다면 학생의 IQ가 125 이상이라는 정보가 0.55라는 대학입학의 확률을 바꾸게 되는가?
A=임의 학생 대학합격률55%, B=IQ125이상

A=0.55 B=0.44 Bc=0.56
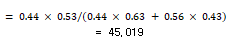
약 45.0% 확률
